Perímetro
|
En matemáticas, el perímetro es la suma de las longitudes de los lados de una figura geométrica. |
Aplicaciones prácticas
El perímetro y el área son magnitudes fundamentales en la determinación de un polígono o una figura geométrica; se utiliza para calcular la frontera de un objeto, tal como una valla. El área se utiliza cuando podemos obtener la superficie interior de un perímetro que se desea cubrir con algo, tal como césped o fertilizantes.
En el uso militar, el término perímetro define una área geográfica de importancia, como una instalación física o trabajo de la defensiva.
Ecuaciones
Perímetro
El perímetro de un polígono se calcula sumando las longitudes de todos sus lados. Así pues, la fórmula para los triángulos es:
P = a + b + c
donde 
, y 
son las longitudes de cada lado. Para los cuadriláteros, la ecuación es:
P = a + b + c + d.
Como tambien podemos decir:
Perímetro: es la suma de los lados de una figura geométrica. Es su contorno.
Ejemplos:
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
|
10 cm
|
 |
|
10 cm
|
El perímetro del rectángulo lo obtenemos sumando todos sus lados:
|
Perímetro = 10 cm + 5 cm + 10 cm + 5 cm = 30 cm
|
Por lo tanto, el perímetro del rectángulo es 30 cm.
Respecto al cuadrado, el perímetro (la longitud de su contorno) se obtiene sumando sus cuatro lados
En la figura, los lados del triángulo miden 4 m.
 |
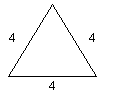Para obtener el perímetro sumamos sus lados:
|
Perímetro = 4 m + 4 m + 4 m = 12 m
|
El perímetro del triángulo es 12 m
Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.
Área de un rectángulo
 |
El área del rectángulo corresponde a la medida de la región verde, y se obtiene multiplicando la base por la altura.
|
Área = base · altura
|
Ejemplo:
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
|
10 cm
|
La altura de este rectángulo mide 5 cm. |
 |
|
|
10 cm
|
La base de este rectángulo mide 10 cm. |
|
Área = 10 · 5 = 50 cm2
|
el área del rectángulo es 50 cm2
|
El centímetro cuadrado (cm2) es una unidad que nos permite medir áreas. También pueden ser metros cuadrados (m2), milímetros cuadrados (mm2), etc.
|
Área del cuadrado
El área de un cuadrado es igual al producto de lado por lado.
Área de un triángulo
El área de un triángulo es igual a la mitad de su base por la altura.
Ejemplos:
Si la base de un triángulo mide 10 cm y su altura mide 5 cm., entonces el área del triángulo es 25 cm2
Tema Perimetros basicos:
Perímetro de un triangulo
| Triángulo Equilátero | Triángulo Isósceles | Triángulo Escaleno |
 |
 |
 |
 |
 |
 |
Perímetro de un cuadrado
Ejemplo
Calcular el perímetro de un cuadrado de 5 cm de lado.
P = 4 · 5 = 20 cm
Perímetro de un rectángulo
Ejemplo
Calcular el perímetro de un rectángulo de 10 cm de base y 6 cm de altura.
P = 2 · (10 + 6) = 32 cm
Perímetro de un rombo
Ejemplo
Calcular el perímetro de un rombo sabiendo que la diagonales miden 30 y 16 cm.
P = 4 · 17 = 68 cm
Perímetro del romboide
P = 2 · (a + b)
Ejemplo
Calcular el perímetro de un romboide de 4 y 4.5 cm de lados y 4 cm de altura.
P = 2 · (4.5 + 4) = 17 cm
Perímetro de un pentágono regular
Perímetro de un hexágono regular
Perímetro de un polígono regular
n es el número de lados
Perímetro de un círculo
Longitud de una circunferencia
Ejemplo
1º Calcular la longitud de una rueda de 90 cm de diámetro.
1º A partir del diámetro
2º A partir del radio
